
Современная теория узлов – это бурно развивающаяся область математики, имеющая также приложения в физике, биологии, генетике и химии.
Теория узлов означает изучение вложений одномерных многообразий в трёхмерное евклидово пространство или в сферу S3. В более широком смысле предметом теории узлов являются вложения сфер в многообразия и вложения многообразий в целом.
В теории узлов число пересечений узла — это наименьшее число пересечений на любой диаграмме узла. Число пересечений является инвариантом узла. Например, тривиальный узел имеет нулевое число пересечений, число пересечений трилистника равно трём, а число пересечений восьмёрки равно четырём.
Узел же в математике – это вложение окружности (одномерной сферы) в трёхмерное евклидово пространство, рассматриваемое с точностью до изотопии. Он является основным предметом изучения теории узлов. Два узла топологически эквивалентны, если один из них можно деформировать в другой, причём в процессе деформации не должно возникать самопересечений.
Частным случаем является вопрос о распознавании тривиальности того или иного узла, то есть о том, является ли заданный узел изотопным тривиальному узлу (можно ли его развязать). Для определения того, является ли конкретный узел тривиальным, можно использовать различные инварианты узлов, например, многочлен Александера или фундаментальную группу дополнения.
Если выбрать систему координат в пространстве, то узел можно задать набором из трех гладких периодических функций: x (u), y (u), z (u). Тогда кратко математические формулы узлов можно записать следующим образом:
ТРИВИАЛЬНЫЙ УЗЕЛ
x = cosu,
y = sinu,
z = 0.

ТРИЛИСТНИК
x = (2 + cos 3u) cos 2u,
y = (2 + cos 3u) sin 2u,
z = sin 3u

Так получилось, что математики долго игнорировали узлы. Первым опубликовал работы на эту тему в конце XVIII века Александр Теофил Вандермонд, французский математик, известный главным образом благодаря работам по высшей алгебре, особенно по теории детерминантов. В честь Вандермонда был назван специальный класс матриц — матрицы Вандермонда, а также элементарное равенство в комбинаторике — свёртка Вандермонда.
В начале XIX века наброски и расчеты узлов выполнил юный Гаусс. Тот самый Иоганн Карл Фридрих Гаусс, немецкий математик, механик, физик, астроном и геодезист, который считается одним из величайших математиков всех времён, «королём математиков». И только в ХХ веке математики всерьез взялись за дело. Но вплоть до середины 80-х гг. теория узлов оставалась всего-навсего одной из ветвей топологии: достаточно разработанная, но интересующая лишь узкий круг специалистов (в основном немецких и американских). Сегодня отношение к теории узлов коренным образом изменилось. Узлы — точнее, математическая теория узлов — интересуют многих биологов, химиков, физиков и даже генетиков.
Интересно отметить, что первые серьезные результаты математической теории узлов получены не математиком, а физиком – Уильямом Томсоном (более известным как лорд Кельвин). Точкой отсчета была его идея сделать узел моделью атома. Моделью, которую впоследствии окрестили «атомом-вихрем» (vortexatom). Для построения теории материи с этой точки зрения необходимо было начинать с изучения узлов. Однако теория Кельвина не развилась и скоро была забыта, оставив, правда, в наследство ряд проблем («гипотезы Тейта»), которые физики тогда не смогли разрешить, но с которыми математики сумели разобраться спустя столетие.
Нельзя не упомянуть о фундаментальной связи между узлами и косами, открытой американцем Джоном Александером, спустя полвека после неудачного старта Кельвина. Алгебраическая теория кос, разработанная в свое время совсем еще юным немецким математиком Эмилем Артином (Emil Artin), более алгебраична, чем геометрическая теория узлов. Эта связь (геометрическая суть которой проста: «замыкание косы») позволила получить основной результат Александера: все узлы отталкиваются от кос. И поскольку классификация кос была быстро получена Артином, была сделана, конечно же, попытка вывести из нее классификацию узлов. Усилия в этом направлении не привели к цели, но породили ряд красивых результатов.
Существует также очень простая геометрическая конструкция, принадлежащая немецкому математику Курту Рейдемейстеру (Kurt Reidemeisteг). Эта идея позволяет свести изучение узлов в пространстве к изучению их проекций (так называемых диаграмм узлов) на плоскости. В итоге она привела ученого к теории катастроф, кодированию узлов и обработке узлов с помощью компьютера.
Известен также алгоритм, изобретенный соотечественником Рейдемейстера Вольфгангом Хакеном (Wolfgang Haken), который позволяет определить, можно или нельзя развязать данный узел. Но этот алгоритм очень сложный. Дело в том, что иногда, чтобы распутать узел, нужно сначала его еще больше запутать. Пример тривиального узла, который не упрощается (его можно развязать, только увеличив сначала число перекрестков) представлен на рисунке.
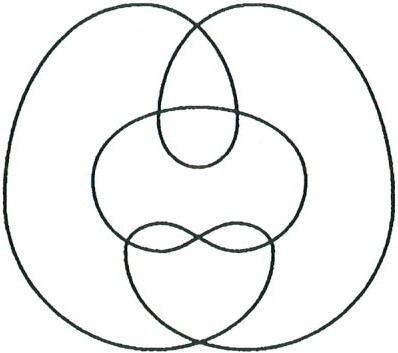
Нужно сказать, что в дальнейшем придумывание плохо распутываемых тривиальных узлов стало важной частью исследований алгоритмов распутывания. Особенно яркий пример узла такого типа (очень трудного для распутывания, и потому не случайно названного Гордиевым), показан на рисунке.

Применяется в науке также и термин «арифметика узлов». Основная теорема арифметики узлов (существование и единственность разложения узла на простые множители) была доказана в 1949 г. немцем Хорстом Шубертом (Horst Schubert). Подозрительное сходство между множеством узлов, наделенным операцией композиции (которая состоит, просто-напросто, в завязывании узлов последовательно один за другим), и множеством натуральных чисел с операцией умножения — породила различные надежды. Например, не являются ли узлы не чем иным, как геометрическим кодированием чисел, не сведется ли классификация узлов к банальному пересчету. К счастью, эти сомнения математиков были вскоре развеяны.
Весьма интересно и полезно изобретение, на первый взгляд тривиальное, англо-американца Джона Конвея (John Conway), одного из наиболее оригинальных математиков прошлого века. Речь идет о новых небольших геометрических операциях над диаграммами узлов. В отличие от операций Рейдемейстера, они позволяют изменять не только вид диаграммы узла, но также и тип узла, а иногда преобразовывают его в зацепление. С их помощью можно определять и вычислять полином Александера-Конвея узла (или зацепления). Эти операции дают очень удобный и достаточно эффективный метод доказательства того, что два узла имеют разный тип и, в частности, что некоторые узлы не могут быть развязаны.
И все-таки, на мой взгляд, больше всего читателей может заинтересовать не этот метод, а биологическое отступление, в котором объясняется, что операции Конвея описывают действие топоизомераз (недавно открытых особых ферментов) на молекулярном уровне. Мне как человеку, активно увлекающемуся ДНК-генеалогией (по сути «молекулярной историей»), буквально недавно написавшему книгу «Древнейшая история Пензенского края: мифы и реальность», где история рассматривается с точки зрения именно новейших исследований ДНК-генеалогии, было особенно интересно самому вникнуть в эту тему и познакомить с ней моих читателей.
Как известно, ДНК состоит из 46 хромосом (23 пары). Все 46 хромосом в итоге состоят из 3 миллиардов нуклеотидов (или нуклеотидных пар), и в их составе находятся примерно 30 тысяч генов. Стало быть, в среднем на одну хромосому приходится 65 миллионов нуклеотидов и 652 гена. Автор множества книг по генеалогии, учёный с мировым именем, доктор химических наук, профессор Гарвардского университета и основатель науки ДНК-генеалогии Анатолий Клёсов в 2006 году ввел термин «ДНК-генеалогия» для изучения мужской Y-хромосомы. При этом точно известно, что в Y-хромосоме содержится 58 миллионов нуклеотидов и всего 40 ген. ДНК-генеалогия рассматривает закономерности наследования изменений нерекомбинантных (негенных) участков ДНК человека в ходе его эволюции на шкале времени от десятков и сотен лет до миллионов лет. Другими словами, ДНК-генеалогия изучает динамику накопления мутаций в ДНК человека, используя подходы химической и биологической кинетики, которые в свою очередь являются частью физической химии. Важнейшая особенность методологии ДНК-генеалогии – определение констант скоростей мутаций в ДНК (в первую очередь в тандемных повторяющихся последовательностях Y-хромосомы, так называемых маркерах, которых, по оценкам, имеется примерно 2500, а также накопления снипов (необратимых мутаций в ДНК) и приложение этих констант к расчетам хронологии древних событий – древних миграций человека, времен жизни общих предков изучаемых популяций.
Вот как сам Анатолий Клёсов определяет суть основополагающих понятий ДНК-генеалогии и, в частности, ее прикладной науки — молекулярной истории: «Суть понятия молекулярной истории в том, что становится возможным следить за передвижениями древних народов не с помощью лопаты и кисточки археолога, не обмеряя черепа, не хитроумно расплетая созвучия и значения слов в живых и мертвых языках, не изучая древние фолианты в библиотеках и монастырях, а прослеживая за метками в Y-хромосомах наших ДНК. Они, эти метки, не могут «ассимилироваться», или «поглотиться» другими языками, культурами или народами, как это происходит тысячелетиями с языками, культурами, народами в рамках понятий истории, лингвистики, этнографии, антропологии. Иначе говоря, методология новой исторической науки, «молекулярной истории», или ДНК-генеалогии, основывается на изучении молекул нуклеиновых кислот, а именно ДНК, дезоксирибонуклеиновой кислоты, в человеческих организмах, как живых, так и в древних костных останках. То, что еще несколько лет назад казалось каким-то развлечением, оказалось, дает истории, антропологии, археологии, лингвистике возможность проверить концепцию, рассмотреть данные под принципиально другим углом, связать воедино, казалось бы, разрозненные части общей картины наших знаний об окружающем мире».
Важность молекулы ДНК, открытой Уотсоном и Криком, — молекулы, несущей генетический код — поставила перед биохимиками целую серию топологических проблем. Эта длинная закрученная двойная спираль может, как известно, воспроизводить свою копию, затем разделяясь в две одинаковые молекулы, которые — в отличие от двух нитей исходной молекулы — не зацеплены между собой и могут разойтись. Как это возможно топологически?
Достаточно тонкие исследования показали, что существуют ферменты, выполняющие эту задачу. Они называются топоизомеразами. Точнее, топоизомеразы позволяют осуществлять три основных операции, представленные на рисунке.
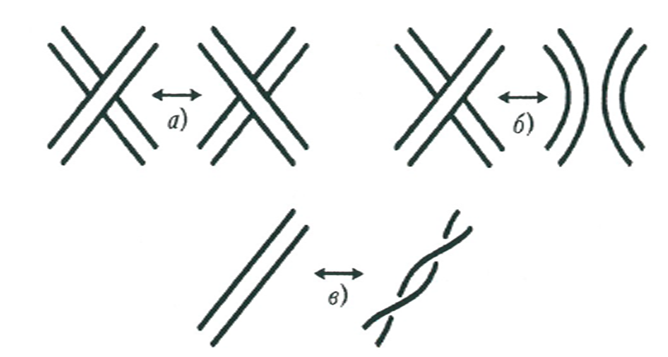
Просвещённые читатели наверняка сразу же узнают операции а) и б) — это, конечно, переброска и разрешение Конвея. Третья операция, которая называется твист, также известна в топологии; она имеет отношение к математической теории лент, весьма полезной в современной теоретической физике. Тем же, кто не знаком с переброской и разрешением Конвея, напоминаю эти операции на конкретных рисунках.
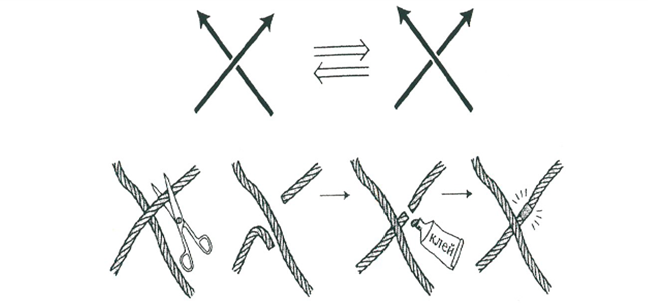
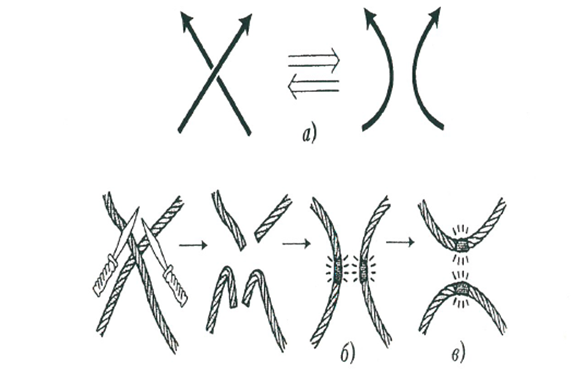
Первая операция, которую мы назвали переброской, состоит в преобразовании выбранного перекрестка в противоположный перекресток – верхняя ветвь становится нижней и наоборот. С веревкой переброска может быть реализована разрезанием верхней ветви и склеиванием ее под второй ветвью.
Вторая малая хирургическая операция – разрешение перекрестка – состоит в ликвидации пересечения путем взаимной замены ветвей. С веревкой она реализуется разрезанием обеих ветвей в точке пересечения и последующим склеиванием их «наоборот».
Переброска и разрешение были известны и часто использовались топологами и до Конвея. В частности, американец Александер использовал их для вычисления полиномов, носящих его имя. Вклад Конвея состоял в том, что он показал, что эти две операции можно использовать в качестве базы для определения инварианта узлов совершенно элементарным образом (полином Конвея).
Рассмотрим более детально, как действуют эти необычные ферменты — топоизомеразы — на длинные молекулы, в частности на молекулы ДНК. Нужно сразу же подчеркнуть, что наблюдать визуально это действие, происходящее на молекулярном уровне, невозможно: даже самые мощные электронные микроскопы позволяют получить лишь косвенные сведения. Напомним вначале, что молекула ДНК представляет собой длинную двойную спираль, каждая нить которой состоит из оснований А, Т, Г, Ц, порядок которых на нити кодирует генетические свойства индивидуума (это похоже на то, как порядок цифр О, 1, 2, …, 9 в строке текста дает десятичный код числа). На рисунке ниже схематично представлена часть молекулы ДНК.
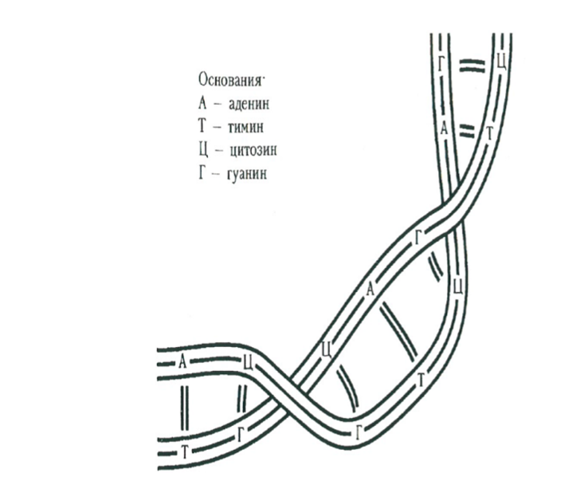
Известно, что концы двух нитей ДНК обычно свободны. Существуют и молекулы из двух замкнутых нитей (две сплетенные змеи, кусающие свои хвосты), а также молекулы, состоящие из единственной нити, как замкнутой, так и со свободными концами. Эти молекулы участвуют в трех классических генетических процедурах: репликации, транскрипции и рекомбинации; кроме того, молекулы из двух нитей способны свертываться (превращаться из вытянутых в компактно упакованные объекты). Топоизомеразы играют решающую роль во всех этих процессах, осуществляя операции разрезания, перекомпоновки и склейки. Во-первых, они могут разрезать нить, переместить другую нить через полученное отверстие и затем заклеить разрез (переброска Конвея). Кроме того, осуществив два разреза и два склеивания, они соединяют две нити «наоборот» (разрешение Конвея).
Точный механизм операций разрезания, передвижения и склейки сегодня еще недостаточно изучен. Тем не менее, известно, что существуют различные типы топоизомераз (они разные для ДНК из одной и двух нитей). В работе Джеймса Ванга (James Wang) описано, как происходит свертывание (и обратная процедура) замкнутой молекулы ДНК.
Свертывание ДНК похоже на то, что часто происходит с телефонным шнуром в форме длинной спирали. Когда вы после разговора опускаете трубку на аппарат, подводящий шнур немного подкручивается, постепенно запутываясь все больше и больше, и становится бесформенным компактным клубком. Это, конечно, досадно, поскольку сокращается расстояние, на которое можно отойти от аппарата. Свертывание ДНК также преобразует длинную спираль в компактный клубок, но в данном случае это полезный результат: преобразование длинной молекулы (длина которой несколько сантиметров) в маленький клубок позволяет ей легко войти в ядро клетки, размеры которого измеряются в ангстремах (один ангстрем есть одна десятимиллиардная доля метра).
В своем нормальном состоянии (не свернутом) спираль ДНК делает полный оборот на протяжении части нити, содержащей 10,5 последовательных оснований. Осуществляя твист большое число раз (см. рис. Схемы операций – пункт в), соответствующие топоизомеразы преобразуют простую замкнутую кривую ДНК так, как это показано на рисунке ниже.
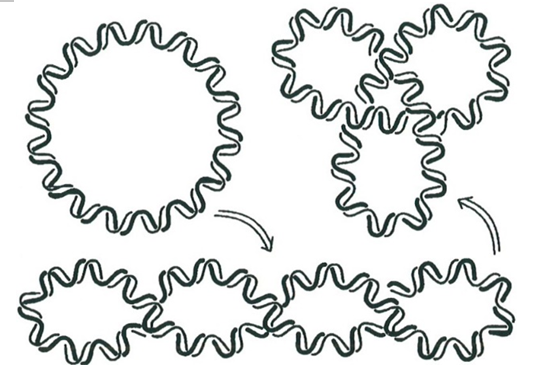
Отметим, что с топологической точки зрения одним из результатов твиста является изменение индекса зацеплений двух ветвей ДНК (этот инвариант, восходящий к Гауссу, измеряет, сколько раз одна ветвь оборачивается вокруг другой). Существуют и другие топологические явления, которые играют существенную роль в биологии; однако детальное описание полученных здесь результатов не входит в наши намерения. Более полную информацию читатель может найти в статье Ванга (Wang, 1994).
В математической теории узлов важное место занимает самый знаменитый инвариант узлов — полином Воана Джонса (Vaughan Jones), который двадцать лет назад привел к тому бурному развитию теории, о котором говорилось выше. Кроме всего прочего, он позволил многим исследователям установить первые серьезные связи теории узлов с физикой. Удивительно, что физическая интерпретация (в статистической физике) полинома Джонса дает вполне элементарное описание инварианта Джонса, первоначальное чисто математическое определение которого было достаточно сложно. Это описание использует очень простой инструмент, который, тем не менее, играет важнейшую роль в современной теоретической физике, — скобку Кауффмана.
Одно из последних великих изобретений теории узлов — инварианты Васильева. Как и в других случаях, исходное определение было весьма сложным. Оно использовало технику теории катастроф и аппарат спектральных последовательностей. Теперь имеется и элементарное описание этих инвариантов. Вместо сложных математических формул читатель может встретить простенькие вычисления с маленькими диаграммами, а также отступление про «социологический» подход к математике.
Таким образом, теория узлов, дебют которой состоялся почти сто пятьдесят лет назад, развивалась затем благодаря настойчивым усилиям математиков, которыми управляло стремление к научным истинам и чисто интеллектуальное любопытство. Чтобы продвигаться, нужны были новые конкретные идеи. И они возникали в воображении лучших исследователей, порождая каждый раз новые надежды и планы на все новые и новые исследования. А каждая неудача позволяла лучше сконцентрироваться на нерешенных проблемах, заманчиво высвечивая все еще не достигнутую цель.
Сегодня мы находимся в положении, близком к сложившемуся в 1860 году. Многие исследователи полагают, как полагал в свое время Уильям Томсон, что узлы играют ключевую роль в фундаментальной физической теории, описывающей структуру материи. Однако это не возвращение к начальной точке. Здесь спираль познания совершила полный виток, и мы обнаруживаем себя в том же положении, но на более высоком уровне.
Теория узлов остается живой и загадочной. Главные проблемы по-прежнему открыты: узлы продолжают ускользать от попыток их ясно классифицировать, и по-прежнему неизвестно, обладают ли они легко вычислимой полной системой инвариантов. И наконец, та фундаментальная роль, которую, как полагают, они играют в физике, еще до конца не определилась.
А в завершении этой главы хотел бы еще раз акцентировать внимание читателей на полезности ДНК-генеалогии. Кто всерьез заинтересовался этой темой, может самостоятельно начать ее изучение на основе трудов одного из ее создателей и активных распространителей Анатолия Алексеевича Клёсова, либо прочитать мою книгу «Древнейшая история Пензенского карая: мифы и реальность», вышедшую в 2020 году, где кратко изложены «20 основных постулатов ДНК-генеалогии». А в разделах «История края на примере выводов ДНК-теста» и «Еще немного о ДНК-генеалогии» достаточно подробно рассказано об этой феноменальной науке.
Интересно!